3 Basics

Um die Ergebnisse dieses Kapitels zu reproduzieren muss nur der Code aus den Chunks in ein eigenes Rmardown File kopiert werden. Das gilt für alle weiteren Kapitel.

Der verwendete Datensatz kann direkt von Github heruntergeladen werden und umfasst eine Vorauswahl an Variablen des European Social Survey (round 8). Diese sind wie folgt kodiert:

country: Land der Befragung
gender: Geschlecht [Weiblich, Männlich]
age: Lebensalter
edu: Höchster Bildungsabschluss (ISCED) [1-7]
income: Netto Haushaltseinkommen in Dezentile (1-10 Kategorien zu einkommen in 10% Schritten)
pol_inter: Politisches Interesse [1: überhaupt nicht interessiert; 4: sehr interessiert]
left_right: Selbsteinschätzung Links-Rechtsskala [1: Links, 10: Rechts]
gay_tolerance: Lesben und Schwule können sich frei entfalten [1: lehne ab; 5: stimme zu]
religious: Religiosität [1: gar nicht, 5: sehr]
imm_poor: Armutsmigration von außerhalb Europas [1: Keine, 4: Viele]
imm_econ: Ist Einwanderung gut oder schlecht für die Wirtschaft? [0: schlecht, 10: gut]
fake_refugee: Meisten Flüchtlinge sind nicht wirklich verfolgt [1: Stimme nicht zu, 5: Stimme zu]
safety: Fühlst du dich nachts sicher? [1: Sehr unsicher; 4: Sehr sicher]
party_right: Identifikation mit einer populistischen Partei (europaweit) […]
vote_right: Indikator - Identifikation mit einer populistischen Partei (europaweit) [0, 1]
party_ger: Parteiidentifikation (DE) [Linke, Grüne, SPD, Union, AfD]
EU_accession: Jahr des EU-Beitritts (eines Landes)
pc: Post-kommunistische Staaten

Der original ESS-Datensatz der mittlerweile 8 Erhebungswelle kann Hier herunter geladen werden.

# load data
load(url('https://github.com/systats/workshop_data_science/raw/master/Rnotebook/data/ess_workshop.Rdata'))
# filter data

library(dplyr)
ess_ger <- ess %>%
  dplyr::filter(country == "DE")

glimpse(ess_ger)

## Observations: 2,852
## Variables: 19
## $ country       <chr> "DE", "DE", "DE", "DE", "DE", "DE", "DE", "DE", ...
## $ gender        <fctr> Male, Male, Male, Male, Male, Male, Female, Fem...
## $ age           <dbl> 22, 58, 64, 52, 67, 73, 34, 40, 77, 30, 41, 70, ...
## $ edu           <dbl> 4, 4, 9, 4, 9, 4, 8, 5, 4, NA, 4, 5, 4, 4, 4, 5,...
## $ income        <dbl> 6, NA, 4, NA, 10, 3, 8, 6, 6, NA, NA, 1, 7, 4, 7...
## $ pol_inter     <dbl> 2, 4, 4, 2, 4, 1, 2, 3, 4, 2, 4, 2, 4, 2, 3, 1, ...
## $ left_right    <dbl> 2, 5, 5, 8, 7, 5, 6, 3, 6, 5, 0, 4, 3, 4, 3, 5, ...
## $ gay_tolerance <dbl> 4, 5, 4, 5, 4, 4, 5, 5, 4, 3, 5, 4, 5, 4, 5, 5, ...
## $ religious     <dbl> 1, 6, 8, 6, 5, 0, 3, 7, 7, 2, 9, 0, 6, 6, 8, 7, ...
## $ imm_poor      <dbl> 3, 4, 5, 5, 3, 2, 4, 5, 4, 5, 4, 4, 2, 4, 5, 4, ...
## $ imm_econ      <dbl> 8, 9, 8, 5, 6, 0, 5, 8, 5, 8, 5, 5, 4, 9, 8, 7, ...
## $ fake_refugee  <dbl> 4, 3, 3, 5, 4, 5, 4, 2, 3, 2, 4, 4, 4, 4, 2, 4, ...
## $ safety        <dbl> 3, 4, 3, 4, 3, 4, 3, 3, 2, 3, 3, 3, 4, 2, 4, 3, ...
## $ party_right   <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, ...
## $ vote_right    <fctr> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
## $ party_ger     <fctr> SPD, SPD, SPD, NA, FDP, NA, NA, SPD, Union, NA,...
## $ region        <chr> "Germany", "Germany", "Germany", "Germany", "Ger...
## $ EU_accession  <fctr> 1958, 1958, 1958, 1958, 1958, 1958, 1958, 1958,...
## $ pc            <chr> "West", "West", "West", "West", "West", "West", ...

Lineare Regression ist das mit Abstand am häufigsten genutzte statistische Modell der empirischen Sozialforschung. Das gilt so gut wie für jede Wissenschaft von der Biologie bis Terrorbekämpfung, da es weniger komplex und einfacher zu interpretieren ist. Allgemein kann damit der Zusammenhang von einer oder mehrerer unabhängigen Variablen \(x\) und einer metrischen, abhängigen Variable \(y\) “erklärt” werden. In den Sozialwissenschaften wird solch ein kausaler Zusammenhang durch theoretische Hypothesen im Vorfeld gut begründet und durch Literaturverweise gestützt.

Eine beispielhafte Hypothese könnte lauten:

\(H_1\): Je höher die Bildung einer Person, desto höher ist ihr Einkommen.

Dieser Zusammenhang soll im folgenden näher betrachtet und geschätzt werden.

3.1 Geometrie

Bevor wir zur mathematischen Notation kommen schauen wir uns die geometrische Form einer Regression an. Im bivariaten Fall, mit nur einer x (edu) und y (income) Variable wird eine Regressionsgerade geschätzt, welche die optimale Linie darstellt, welche von allen Datenpunkten im Durchschnitt gleich weit entfernt ist.

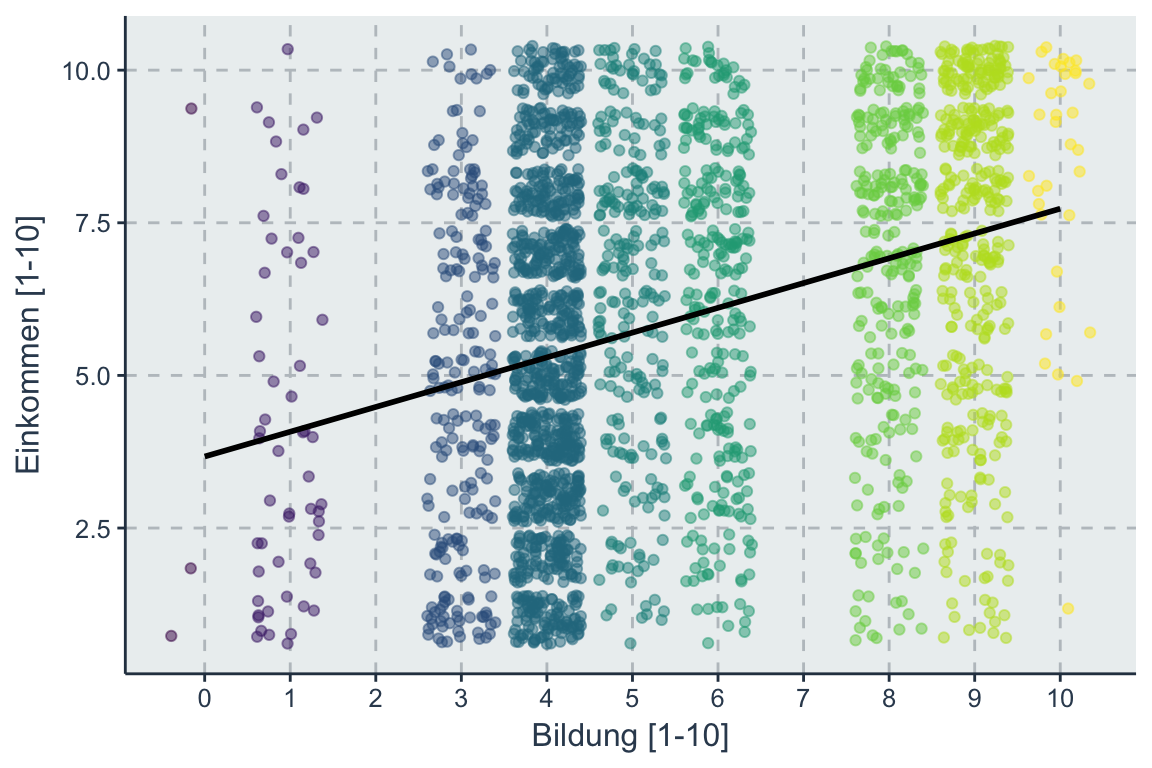
Figure 3.1: Soziale Mobilität durch Bildung

Statt eine Streudiagramms oder Scatterplots kann man auch einen Boxplot nutzen um den Zusammenhang zwischen Bildung und Einkommen visuell zu untersuchen.

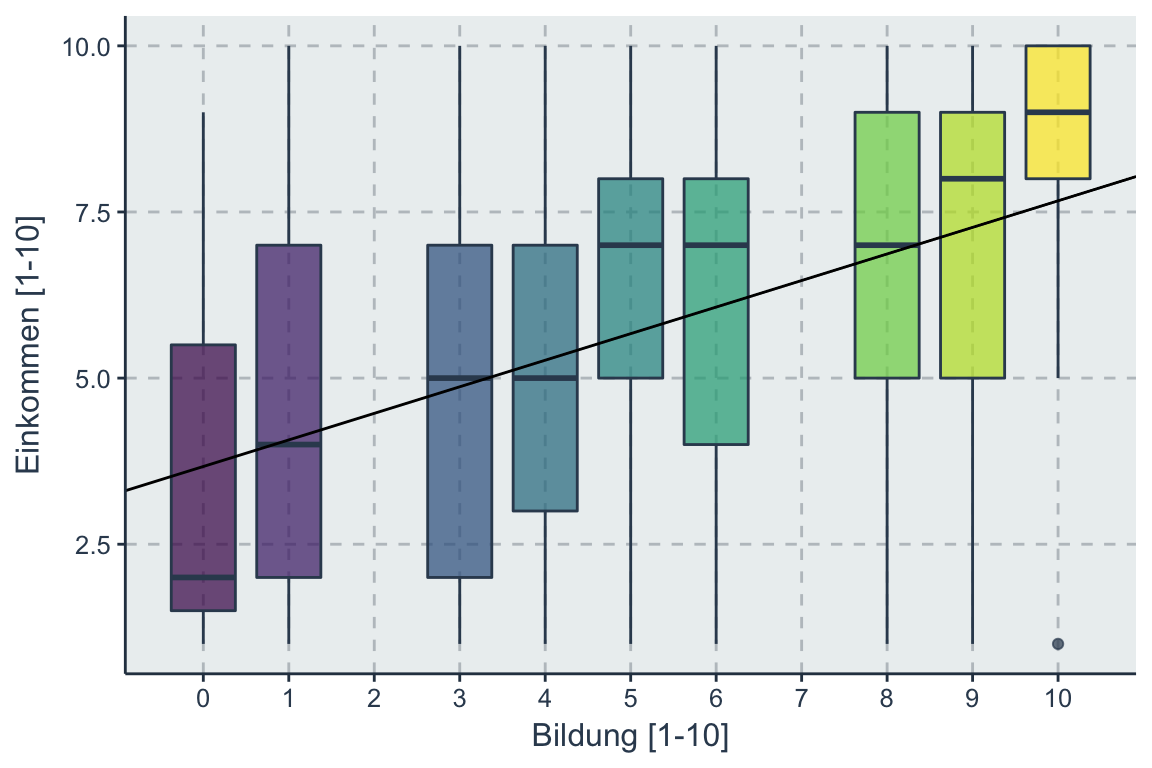
Die Regressionsgerade schätzt für jede Ausprägung von Bildung einen Mittelwert der zu einer Regressiongerade über alle Ausprägungen hinweg generalisiert wird.

Bei rpsychologist wird der Mechanismus nochmals verdeutlicht.

3.2 Simple Lineare Regression

Mathematische Notationen helfen dabei statistische Konzepte besser zu verstehen und die eigenen Modellierungen für andere zu dokumentieren. Eine einheitliche Notation gibt es allerdings nicht.

In der Algebra wird eine Gerade definiert durch

\[y = mx + b \] wobei m die Steigung und b den y-Achsenabschnitt angibt. Die Steigung m (engl. Slope) ergibt sich aus

\[m = \frac{rise}{run} = \frac{\text{change in y}}{\text{change in x}} = \frac{\Delta Y}{\Delta X} = \beta_1\]

In der Statistik wurden über die Jahrzehnte unterschiedliche Schreibweisen eingeführt die sich jedoch nur formal und nicht inhaltlich unterscheiden. So wird der y-Achsenabschnitt der Regressionsgerade (engl. Intercept) an erster Stelle mit \(\beta_0\) beschrieben. Hinzu addiert wird die Steigung \(\beta_1\) multipliziert mit der x-Ausprägung. Da die Regressiongerade nur eine lineare Schätzung darstellt bleibt bei den meisten Fällen noch ein individueller Fehler \(\varepsilon_i\) (Residuen) für jede Beobachtung übrig der nicht “erklärt” werden konnte.

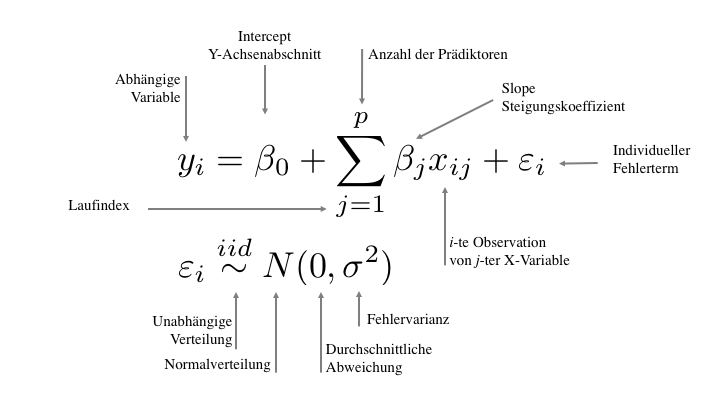
Diese Gleichung wird unterschieden in

Strukturelle Komponente \(\hat y_i = \beta_0 + \beta_1x_i\) und
Residuen \(\varepsilon_i \sim N(0, \sigma^2)\)

\(\hat y\) ist die Regressiongerade und \(\hat y_i\) ist der individuelle Vorhersagewert welcher durch die Parameterkonstellation kalkuliert wird. Die Distanz zwischen den Beobachtungen und geschätzten Werten \((y_i - \hat y_i) \sim N(0, \sigma^2)\) werden als zufälliger Fehler betrachtet, welcher idealerweise normalverteilt um die Regressionsgerade streut (idiosynkratisch).

Mathematisch betrachtet wird die theoretische Hypothese von Anfang in eine Formel übersetzt

\[\text{Einkommen}_i = \beta_0 + \beta_1 \text{ Bildung}_i + \varepsilon_i\]

Nun schätzen wir diese Formel mit Hilfe von R. Regressionsformeln werden in R durch die sogenannte formula definiert. In die Funktion lm (linear model) wird erst die Y und dann die X Variable(n) geschrieben. Das Symbol ~ (Tilde) wird anstelle des mathematischen ist gleich = genutzt. Zuletzt folgt durch ein Komma getrennt der Datensatz. Alle Berechnungen der Regression werden in ein neues Regressionsobjekt fit1 (beliebiger Name) gespeichert. So können Unmengen an Modellen geschätzt und später kompakt verglichen werden (dazu später mehr).

fit1 <- lm(income ~ edu, data = ess_ger)
summary(fit1)

## 
## Call:
## lm(formula = income ~ edu, data = ess_ger)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -6.7307 -2.2952  0.1108  2.1108  5.9226 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.67144    0.14096   26.05   <2e-16 ***
## edu          0.40593    0.02415   16.81   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.648 on 2534 degrees of freedom
##   (316 observations deleted due to missingness)
## Multiple R-squared:  0.1003, Adjusted R-squared:  0.09993 
## F-statistic: 282.5 on 1 and 2534 DF,  p-value: < 2.2e-16

3.3 Interpretation der Koeffizienten

Unsere Regression fit1 hat folgende Parameter geschätzt.

\[Einkommen_i = 3.67 + 0.4*Bildung_i + \varepsilon_i\]

broom::tidy(fit1)

##          term  estimate  std.error statistic       p.value
## 1 (Intercept) 3.6714380 0.14095937  26.04607 1.016797e-132
## 2         edu 0.4059302 0.02415333  16.80638  3.527291e-60

Der Intercept \(\beta_0\) besagt, dass der Erwartungswert für Einkommen bei 3.67, wenn der Einfluss von Bildung (X-Variablen) konstant Null gehalten wird. D.h. jemand ohne Bildungsabschluss hat einen durchschnittlichen Wert von 3.67 auf der Einkommensskala (Achtung mit dieser Interpretation bei Variablen ohne natürlichen Nullpunkt und in multivariaten Modellen!). Die Steigung \(\beta_1\) gibt an, dass eine Erhöhung um einen Bildungsabschluss das Einkommen durchschnittlich um 0.4 Skalenpunkte ansteigen lässt.

Für jeden Parameter wird ebenfalls ein Signifikanztest durchgeführt, welcher sicherstellen soll, dass die statistischen Ergebnisse nicht das Resultat des Zufalls sind. Denn bei jeder Datenerhebung sind zufällige Fehler in der Stichprobe zu erwarten. Dadurch kann nicht per se davon ausgegangen werden, dass ein geschätzter Parameter basierend auf einer zufälligen Stichprobe auch in der Grundgesamtheit (Population) vorzufinden ist.

Beide Tests basieren auf den Standardfehler std.error (SE), welcher die Abweichungen/ Fehlerstreuung um den Parameter beschreibt.

\[SE(\beta_0) = \sigma^2 \left[\frac{1}{n} + \frac{\bar x^2}{\sum^n_{i=1} (x_i - \bar x)^2} \right]\] \[SE(\beta_1) = \sqrt{\frac{\sigma^2}{\sum^n_{i=1} (x_i - \bar x)^2}} = \frac{\sigma}{s_x\sqrt{n}}\] \(\sigma^2 = var(\varepsilon)\) ist die Fehlervarianz.

3.3.1 Logik von Signifkanztest

Die Frage lautet also wie sicher sind wir uns, dass ein geschätzter Parameter signifikant von 0 abweicht und in der Realität wirklich ein Zusammenhang existiert? Antwort auf solche Fragen liefert die Inferenzstatistik, welche eng mit der Wahrscheinlichkeitstheorie verknüpft ist. In der frequentistischen Statistik kommen hauptsächlich zwei Konzepte zum Einsatz:

Konfidenzintervalle
Null-Hypothesentest (NHST)

Beide Konzepte sind schon älter und u.a. umgesetzt im t-Test (für Gruppenmittelwerte). Voraussetzung für diese Signifikanztests ist eine echte Zufallsstichprobe (jedes Element einer Population hat die gleiche Chance in das Sample zu kommen). Das Problem liegt nun darin die gefundenen \(\beta\) Parameter (von den Sample Daten geschätzt) zu generalisieren (auf die Grundgesamtheit).

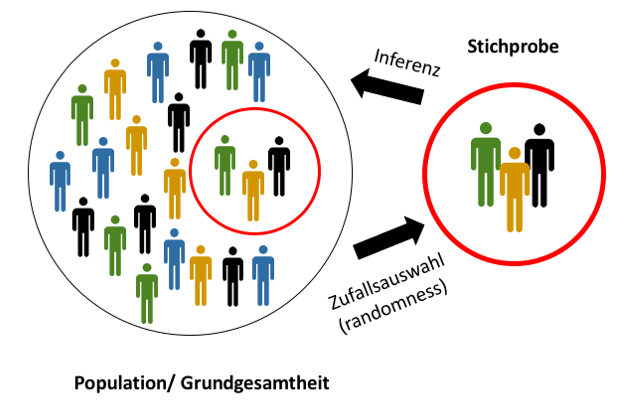
Alle Verfahren benutzen Wahrscheinlichkeitsverteilungen, die wichtigste ist die Normalverteilung.

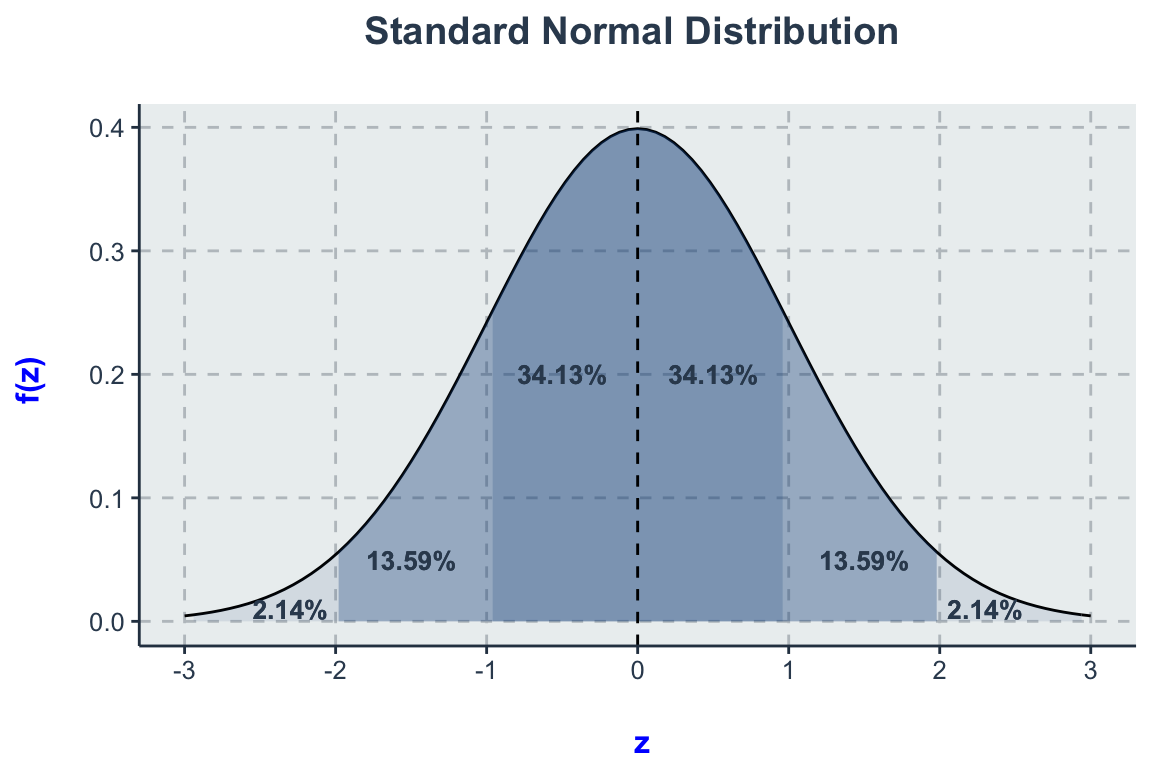
Auch Gauß-Verteilung genannt, ist sie idealtypisch für stetige Verteilungen. Jede Normalverteilung besitzt den Mittelwert (\(\mu\)) und die Varianz (\(\sigma^2\)). Zusätzlich sind alle Normalverteilungen symmetrisch um ihren Mittelwert \(\mu\) und mit zwei fixen Wendepunkten (\(\mu\pm\sigma\); Mittelwert \(\pm\) Standardabweichung). Des weiteren verläuft sie asymptotisch Richtung \(\pm \infty\). Als Standardnormalverteilung wird jene Normalverteilung bezeichnet, die den Mittelwert \(\mu=0\) und \(\sigma^2=1\). Diese kann durch die Standardisierung der X-Werte erreicht werden.

Die Standardabweichung \(\sigma\) beschreibt die Breite der Normalverteilung. Die Halbwertsbreite einer Normalverteilung ist das ungefähr 2,4-fache (genau \(2 \sqrt{2 \ln 2}\)) der Standardabweichung. Es gilt näherungsweise:

Intervall der Abweichung \(\pm \sigma\) vom Mittelwert \(\mu\) sind 68,27 % aller Messwerte
Intervall der Abweichung \(\pm 2\sigma\) vom Mittelwert \(\mu\) sind 95,45 % aller Messwerte
Intervall der Abweichung \(\pm 3\sigma\) vom Mittelwert \(\mu\) sind 99,73 % aller Messwerte.

Und ebenso lassen sich umgekehrt für gegebene Wahrscheinlichkeiten die maximalen Abweichungen vom Mittelwert finden. Daraus lässt sich die 95% Konvention der Sozialwissenschaften ableiten.

50 % aller Messwerte weichen höchstens \(0.675\sigma\) vom Mittelwert \(\mu\) ab
90 % aller Messwerte weichen höchstens \(0.645\sigma\) vom Mittelwert \(\mu\) ab
% aller Messwerte weichen höchstens \(1.960\sigma\) vom Mittelwert \(\mu\) ab
99 % aller Messwerte weichen höchstens \(2.576\sigma\) vom Mittelwert \(\mu\) ab

Aufgrund der Logik von Signifikanztests können mehrere Fehler bei der Zurückweisung von Hypothesen unterlaufen. Insgesamt können vier Ereignisse eintreten.

		Population
		\(H_0\)	\(H_1\)
Stichprobe	\(H_0\)	+	Fehler 2. Art (\(\beta\))
	\(H_1\)	Fehler 1 Art (\(\alpha\))	+ (Testärke/Power)

Fehler 1.Art Bei einem Signifikanzniveau von 5% (Irrtumswahrscheinlichkeit) entscheidet man sich gegen die \(H_0\) obwohl diese richtig ist. Damit würde folglich fälschlicherweise ein Zusammenhang angenommen.

Fehler 2.Art Die \(H_A\) ist richtig, man entscheidet sich aber gegen sie und für die \(H_0\). Hier würde fälschlicherweise kein Zusammenhang angenommen werden.

Je niedriger das Signifikanzniveau angesetzt wird, desto geringer ist die Wahrscheinlichkeit den Fehler 1. Art \(\alpha\) aber umso höher den Fehler 2. Art zu begehen. Mit steigendem Stichprobenumfang werden auch substanziell unbedeutende Effekte signifikant und umgekehrt. Da das Signifikanzniveau stark durch die Fallzahl N beeinflusst wird, sollte bei kleinen Stichprobenumfängen auf die Teststärke kontrolliert werden.

3.3.2 Konfidenzintervall

Der Standardfehler wird genutzt um das Konfidenzintervall (Vertrauens-, Erwartungsbereich) eines Parameters zu konstruiieren. Per Konvention wird in den Sozialwissenschaften das 95% Signifikanzniveau eingesetzt um relevante Effekte zu identifiezieren.

Ein Konﬁdenzintervall ist so konstruiert, dass der wahre Parameter \(\beta_1\) mit der Wahrscheinlichkeit \(1-\alpha\) überdeckt wird. Somit wird davon ausgegangen, dass in 95% der Fälle (bei unendlicher Wiederholung des Zufallsamples^^) die stochastischen Intervallgrenzen den wahren Parameter überlappen. Bzw. nur in 5% der Fälle ist der wahre Populationsparameter außerhalb des Konfidenzintervals zu warten.

\[CI_{\beta} = \hat \beta_1 \pm t_{\frac{\alpha}{2}} \; SE(\beta_1)\]

\[[\hat\beta_1 - t_{\frac{\alpha}{2}} \; SE(\beta_1) \leq \beta_1 \leq \hat \beta_1 + t_{\frac{\alpha}{2}} \;SE(\beta_1)]\] \[[0.4 - 1.96 * 0.02 \leq \beta_1 \leq 0.4 + 1.96 * 0.02]\]

\[[0.35 \leq \beta_1 \leq 0.45]\]

Setzt man den geschätzten Parameter und den Standardfehler in die Formel ein errechnet sich eine untere Intervallgrenze von 0.35 und eine Obere von 0.45 in dem der wahre Effekt von Bildung und Einkommen mit 95% Sicherheit liegt. Da das Konfidenzintervall die Null nicht überlappt ist der positive Effekt von Bildung auf Einkommen statistisch signifikant (5% Irrtumswahrscheinlichkeit). Das lässt sich einfach in R überprüfen.

confint(fit1) # 95 Konfidenzintervall

##                 2.5 %    97.5 %
## (Intercept) 3.3950307 3.9478453
## edu         0.3585679 0.4532925

confint(fit1, level = 0.90) # 90 KI

##                  5 %      95 %
## (Intercept) 3.439496 3.9033803
## edu         0.366187 0.4456734

Wie oben schon gezeigt ist es einfach zu sagen, dass das 95% Konfidenzintervall den wahren Parameter mit einer Wahrscheinlichkeit von 95% beinhaltet (überlappt). Aus einer streng frequentistischen Perspektive wird Parameterunsicherheit jedoch nicht in Wahrscheinlichkeiten gemessen. Stattdessen besagt das Konfidenzintervall, dass bei (unendlicher) Wiederholung der Datenerhebung und Analyse, der wahre Parameter in 95% der Fälle im gegeben Intervall vorzufinden ist.

Praktisch betrachtet kann man auch den Konfidenzintervall mittels Bayesianische Statistik als Wahrscheinlichkeit interpretieren. Das ist deshalb möglich, da Bayesianische Schätzmethoden ähnliche Ergebnisse wie Maximum Likelihood (mit flat Priors) liefert. Also interpretieren wir die frequentistische Maße mittels Bayesianischen Konzepten und das ist sogar noch inntuitiver? Ja, aber: Die Interpretation der Signifikanztest steht am Ende einer ganzen Reihe von Modellspezifikationen und hängt konkret von den vorliegenden Daten, bzw. der Fallzahl \(N\) ab. D.h. man schafft sich eine eigene kleine Modellrealität (interne Validität), die unter Umständen nichts mehr mit realen Welt zu tun hat (externe Validität). Nichtsdestotrotz ist das Konfidenzintervall durch seine Breite ein sehr informativer Wert.

Des Weiteren könnte man die Konvention von \(\alpha=95\%\) kritisieren als dem Hut gezaubert. Ronald Fisher schrieb dazu selbst: The [number of standard deviations] for which P = .05, or 1 in 20, is 1.96 or nearly 2; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not (Fisher 1925: 53). Man kann berechtigterweise in Frage stellen ob Bequemlichkeit als wissenschaliche Kategorie zählt. AAS… statment. God loves

We are not interested in the logic itself, nor will we argue for replacing the .05 alpha with another level of alpha, but at this point in our discussion we only wish to emphasize that dichotomous significance testing has no ontological basis. That is, we want to underscore that, surely, God loves the .06 nearly as much as the .05. Can there be any doubt that God views the strength of evidence for or against the null as a fairly continuous function of the magnitude of p (Rosnow & Rosenthal, 1989).

3.3.3 Nullhypothesentest

Wissenschaftliche Erkenntnisse sind ohne Null-Hypothesentests undenkbar. Erst formulieren Forscher ihre Theorien über die Welt in Arbeitshypothesen (\(H_A\) oder \(H_1\)). Eine Arbeitshypothese impliziert immer auch eine Nullhypothese, die meistens keinen Zusammenhang unterstellt bzw. dass der Parameter (einer Korrelation, einer Regression oder ein Gruppenmittelwertsunterschied) 0 ist, also ein Zusammenhang nicht existiert. Wissenschaftliche Praxis besteht darin Beweise in Form von Daten und statistischer Tests gegen die Nullhypothese zu sammeln. Formal werden hypothesen so definiert, wobei das nur zu Formaliersierung der Logik dient und nicht Teil einer wissenschaftlichen Arbeit.

\[H_0: \beta_1 = 0\] \[H_1: \beta_1 \neq 0 \;\;\; \text{(zweiseitig)}\]

In einer hypothetischen Welt in der die \(H_0\) zu trifft und der Parameter eigentlich 0 ist, wie weit weicht der geschätzte Parameter \(\beta_1\) davon ab?

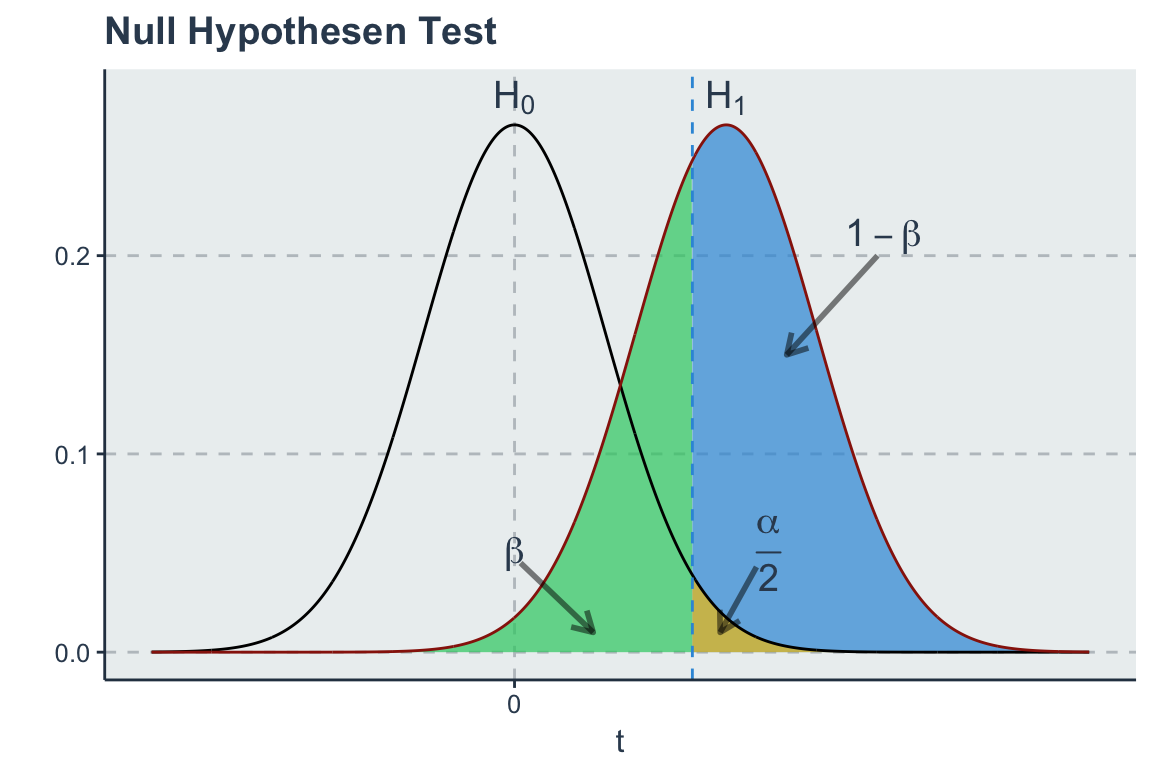
Konvention in den Sozialwissenschaften ist \(|t| > 1,96\) für das 95% Signifikanzniveau. Der t-Wert misst die Distanz von \(\beta_1\) zu 0 in Standardabweichungen.

\[t = \frac{\beta_1 - 0}{SE(\beta_1)} \sim N(0, 1) \text{ genauer }\sim t_{n-2} \]

Dauemnregel: Wenn \(\beta > 2 SE(\beta)\), weicht der Parameter signifikant (95%) von Null ab.

Somit führen größere t-Werte, wie im obigen Beispiel \(t = 0.4059/0.0241 = 16.806\) zu einem signifikanten Ergebnis (\(^{***}\)). Der daraus abgeleitete p-Wert entspricht dem Signifkanzniveau, bei dem \(H_0\) auf Basis der Stichprobenbeobachtung empirisch verworfen wird. Der p-Wert entspricht somit der Wahrscheinlichkeit, dass wir einen Fehler machen, wenn wir \(H_0\) verwerfen, d.h.

\[p = P_{H_0}(|T|>|t|) = 2(1 − \Phi(|t|)) \]

Der sehr kleine p-Wert (p.value) verrät, dass die Evidenz gegen \(H_0\) stark ist und es sehr unwahrscheinlich ist, dass solch einen Effekt basierend auf dem reinen Zufall zu Stande kommt. Der geschätzte Zusammenhang ist statistisch signifikant, was nicht Bedeutsamkeit sondern Sichtbarkeit bzw. Reliabilität ausdrückt.

Parameter	\(\;\;\;\)	Kriterium
\(\beta_0\)		Der Achsenabschnitt sollte nicht interpretiert werden.
\(\beta_1\)		Der unstandardisierte Koefizient kann \(\pm \infty\) groß werden. Je weiter von 0 entfernt desto besser.
\(SE(\beta_1)\)		Der Standardfehler des Steigungsparameters sollte Richtung 0 tendieren. Erst wenn \(SE(\beta_1) > 2 * \beta_1\) wird ein Parameter signifikant.
t-Statistik		Sollte größer als \(t_{crit} =1.96\) um auf 95% Signifikanzniveau die \(H_0\) zu verwerfen

Je größer die t-Statistik desto kleiner der p-Wert.

Rethinking: Is NHST falsificationist? Null hypothesis significance testing, NHST, is o en identified with the falsificationist, or Popperian, philosophy of science. However, usually NHST is used to falsify a null hypothesis, not the actual research hypothesis. So the falsification is being done to something other than the explanatory model. It is seems the reverse from Karl Popper’s philosophy (Statistical Rethinking, 5).

3.4 Dummies

Nominales bzw. qualitatives Messniveaus liegt bei ungeordneten Gruppen oder Klassen von Beobachtungen vor (Beispiele: Geschlecht, Konfessionen, Parteimitgliedschaft, Region, Land etc.). Diese Gruppenvariable wird zur Schätzung in einen s.g. Dummy überführt. Dieser erfordert eine binäre Datenstruktur und wird auch als Indikatorvariable oder als one-hot encoded bezeichnet.

\[ D_i = \left\{ \begin{array}{l} 1:\text{ Beobachtungen einer Gruppe}\\ 0:\text{ den Rest, nicht Teil der Gruppe} \end{array}\right. \]

Technisch betrachtet können auch Variablen mit Text als Ausprägung geschätzt werden, allerdings werden diese durch das statistische Modell in 0 und 1 transformiert. Der Steigungsparameter \(\beta_D\) eines Dummies repräsentiert den Unterschied in der Y-Variable aufgrund der Gruppenzugehörigkeit in \(D\{1, 0\}\). Letztere wird Null- oder Referenzkategorie genannt. Wenn eine Variable \(k\) Gruppen besitzt, werden diese in \(k-1\) Dummyvariablen überführt. Auch ordinale Variablen können so einbezogen werden, allerdings verlieren sie bei der Transformation ihre Ordnungsstruktur und werden als gleiche Klassen behandelt. Beispiel: Geschlecht.

\[ D_i = \left\{ \begin{array}{l} 1:\text{ if male}\\ 0:\text{ if female} \end{array}\right. \]

Für jede der beiden Geschlechtergruppen wird nun ein spezifischer Mittelwert geschätzt. Die Differenz der Mittelwerte drückt sich im Steigungsparameter \(\beta_D\) aus.

fit_gender <- lm(income ~ gender, data = ess_ger)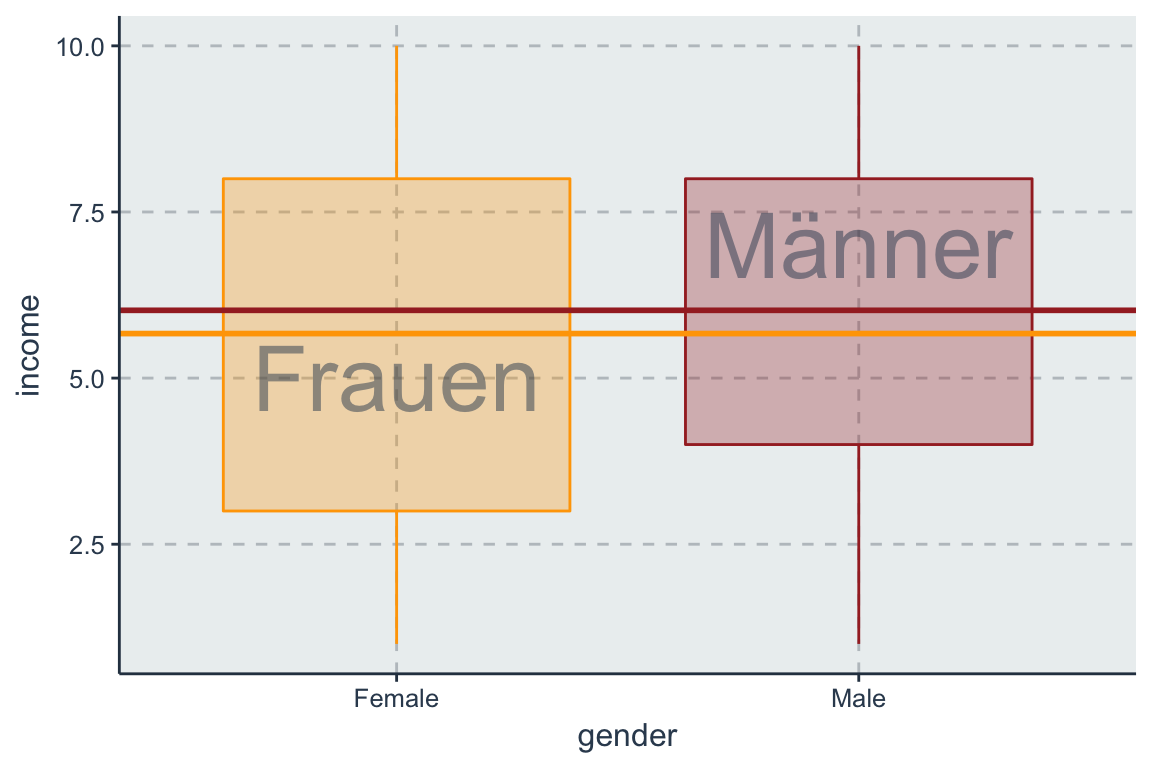

library(tidyr)
tidy(fit_gender)

##          term  estimate  std.error statistic    p.value
## 1 (Intercept) 5.6761032 0.08043671 70.566082 0.00000000
## 2  genderMale 0.3506427 0.11064868  3.168973 0.00154794

Der Intercept bezieht sich immer auf den Gruppenmittelwert der Referenzkategorie 0, also auf Frauen. Demnach entspricht der Parameter dem Unterschied von Männern gegenüber Frauen. Der Parameter genderMale gibt an, dass Männer im Durchschnitt 0.35 Einkommenpunkte als Frauen. Der t-Test mit \(H_0:\beta = 0\) ist identisch mit der Nullhypothese, dass zwei Populationsmittelwerte nicht voneinander abweichen (\(H_0: \mu_1 = \mu_2\)). Erlangt ein Parameter \(\beta\) (\(\mu_1-\mu_2\)) einen hohen empirischen t-Wert \(>|1.96|\), ist der Unterschied der Gruppenmittelwerte signifikant von Null verschieden.

\[ y = \beta_0 + \beta_1 D + \varepsilon_i \]

Im Fall, dass der Dummy \(D\) die Ausprägung 1 annimmt wird folgende Gleichung berechnet:

\(E(y|X, D=1) = \beta_0 +\) \(\beta_1*1\) \(+ \varepsilon\)

\(E(y|X, D=0) = \beta_0 +\) \(\beta_1*0\) \(+ \varepsilon\)

Ein Dummy Variable bewirkt eine Parallelverschiebung der Regressionsgerade um den Mittelwertunterschied \(\beta_D\).

\[\beta_D = E(y|D=1) - E(y| D=0)\]

Bisher wurde eine nominale Kategorie extrahiert [1] und zur Referenzkategorie [0] kontrastiert. Informationen über mögliche andere Kategorien sind nicht mehr vorhanden. Allgemein können Variablen mit k Ausprägungen in \(k\) Dummies überführt werden. Jedoch können nur \(k-1\) in ein Modell aufgenommen werden, da eine Kategorie immer als Referenz-/ Nullkategorie/ Baseline übrig bleiben muss.

\[ \left[ \begin{array}{c} var \\ B \\ A \\ C \\ B \\ C \\ A \\ A \\ \end{array} \right] = \begin{bmatrix} var_A & var_B & var_C \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ \end{bmatrix} \]

Ein Effekt wird immer im Gegensatz (Kontrast) zu dieser Baseline Kategorie interpretiert. Demnach werden von den drei Dummies A, B, C nur zwei ins Modell integriert, da sonst perfekte Multikolinearität vorliegt und die Parameter nicht mehr identifiziert werden können. Die Baseline [0]-Kategorie eines Dummies sollte entsprechend zweier Kriterien ausgewählt werden:

Methodisch: die Fallzahl dieser Kategorie sollte mindestens \(\geq 10%\) aller Fälle umfassen
Analytisch: die Kategorie sollte mit allen übrigen Kategorien inhaltlich vergleichbar sein.

Wenn Variablen mehrere Kategorien umfassen können diese einfach in mehrere Dummies übersetzt werden. Dazu stehen zwei Optionen zur Auswahl:

Für einzelne Variablen

# install.packages("dummies")
library(dummies)
spez <- dummy(ess_ger$gender, 
              sep = "_", 
              fun = as.integer)

# an den Hauptdatensatz anbinden
glimpse(cbind(ess_ger, spez))

für mehrere Variablen gleichzeitig. Numerische aka metrische Variablen werden nicht transformiert und werden unverändert übernommen.

dumy_dat <- dummy.data.frame(ess_ger)

# Welche Variablen sind letztendlich dummy kodiert?
which.dummy(dumy_dat)
get.dummy(dumy_dat) %>% head()

Kaggle notebook visualising categorical features

3.5 Multivariate Regression

Bisher wurde die lineare Regression nur im bivariaten Fall besprochen. Die Forschungspraxis hingegen erfordert multivariate Modelle, um multiple Kausalitäten abbilden zu können. Fügt man eine weitere unabhängige x-Variable hinzu, wird die Regressionsgerade zur Regressionsebene (Fläche). Ab 3D wird es zwar schwer sich vorzustellen, allerdings gelten alle bisherigen Konzepte auch in Vektorräumen n-ter Ordnung.

R ermöglicht es viele Modelle gleichzeitig zu schätzen um sie dann zu vergleichen. Im multivariaten Fall wird jede weitere unabhängige x Variable wird durch ein + getrennt ins Model aufgenommen.

fit0 <- lm(income ~ 1, data = ess_ger) # Nullmodell, univariat
fit1 <- lm(income ~ edu, data = ess_ger) # bivariat
fit2 <- lm(income ~ edu + age, data = ess_ger) # multivariat, trivariat

library(broom)
broom::tidy(fit2)

##          term    estimate   std.error statistic       p.value
## 1 (Intercept)  4.78112568 0.186352311 25.656380 3.018676e-129
## 2         edu  0.43606492 0.024025295 18.150243  2.613696e-69
## 3         age -0.02583209 0.002894054 -8.925919  8.291415e-19

Monokausale Erklärungsansätze sind genauso inadequat the Realität abzubilden wie eine bivariate Regression. Allgemeiner gesagt sollte der kausale Zusammenhang (Data-Generating-Process) richtig spezifiziert werden und mehrere Variablen und Kontrollvariablen umfassen. Eine multivariate Regression schätzt orthogonale Parameter, die nicht mit einander korreliert sind. Man spricht von partiellen oder isolierten Effekten.

Wie werden die Parameter \(\beta_0, \beta_1, \beta_2\) eines multivariaten Modells interpretiert?

\(\beta_0\): Vorhergesagter Wert für Einkommen wenn alle Prädiktoren die Ausprägung 0 annehmen. Diese Interpretation ist nur sinnvoll wenn alle Variablen zuvor mittelwert-zentriert worden sind. In den meisten Fällen jedoch macht dieses Szenario kaum Sinn, bzw. ist es nicht von Interesse. Der Intercept sollte eher als Schätzungshilfe gesehen werden.
\(\beta_1\): Der unstandardisierte Effekt von Bildung auf Einkommen, während die anderen x Variablen konstant 0 gehalten werden (Centeris Paribus). Das Ergebnis ist ein unstandardisierter, partiell (isoliert) geschätzter Steigungsparameter. So wird versucht den eigenen Erklärungsanteil einer Variablen zu isolieren.
\(\beta_k\): siehe \(\beta_1\)

Wie leicht zu sehen ist wird für jede Variable ein Parameter geschätzt, insgesamt also \(k + 1\) (+ Intercept). Auch steht fest \(n >^! k\) (es sind mehr Beobachtungen als Parameter notwendig). Zur Verdeutlichung der multivariaten Konzeption werden die x-Variablen als Matrix zusammengefasst.

\[ \left[ \begin{array}{c} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{array} \right] = \beta_0 + \begin{bmatrix} x_{11} & x_{12} & ... & x_{1k}\\ x_{21} & x_{22} & ... & x_{2k}\\ x_{31} & x_{32} & ... & x_{3k}\\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & ... & x_{nk}\\ \end{bmatrix} \times \left[ \begin{array}{c} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{array} \right] + \left[ \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \vdots \\ \varepsilon_n \end{array} \right] \]

Diese Matrix-Notation kann wiederum in einzelne Vektoren definiert werden.

\[ \left[ \begin{array}{c} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{array} \right] = \beta_0 + \beta_1 \times \left[ \begin{array}{c} x_{11}\\ x_{21}\\ x_{31}\\ \vdots\\ x_{n1}\\ \end{array} \right] + \beta_2 \times \left[ \begin{array}{c} x_{12}\\ x_{22}\\ x_{32}\\ \vdots\\ x_{n2}\\ \end{array} \right] + \beta_p \times \left[ \begin{array}{c} x_{1k}\\ x_{2k}\\ x_{3k}\\ \vdots\\ x_{nk}\\ \end{array} \right] + \left[ \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \vdots \\ \varepsilon_n \end{array} \right] \]

3.6 Standardisierung

Wenn man die Stärke eines Parameters wissen möchte kann man alle X-Variablen z-transformieren um sie vergleichbar zu machen. ACHTUNG: Falls Ausreißer in den Daten sind, werden diese extremen Werte als neue Intervallgrenze [-2,+2] gesetzt. Der Buchstabe z leitet sich aus dem zentralen Grenzwertsatz für Zufallsvariablen ab. Dazu wird die Variable erst zentriert und dann durch die Standardabweichung geteilt.

\[z = \frac{x_i - \bar x}{s_x}\]

In R lässt sich eine Variable sehr einfach transformieren:

scale(ess_ger$edu) %>% head

##            [,1]
## [1,] -0.6207313
## [2,] -0.6207313
## [3,]  1.6782133
## [4,] -0.6207313
## [5,]  1.6782133
## [6,] -0.6207313

oder einfacher in Verbindung mit mutate

ess_ger %>% 
  mutate(edu_z = scale(edu), age_z = scale(age)) %>%
  lm(income ~ edu_z + age_z, data = .)

## 
## Call:
## lm(formula = income ~ edu_z + age_z, data = .)
## 
## Coefficients:
## (Intercept)        edu_z        age_z  
##      5.8597       0.9484      -0.4778

Nun liegt eine Teilstandardisierung zweier Prädikatoren vor. Der Parameter \(\beta_1\) besagt nun, dass wenn edu_z um eine Standardabweichung steigt, income sich um x Einheiten erhöht. Gleiches gilt für age_z. Die Skala der Y-Variable bleibt unverändert. Die Standardisierung der Regressionskoeffizienten eliminiert Skaleneffekte, so dass die Größe eines geschätzten Wertes unabhängig von linearen Transformationen der entsprechenden Messskala vorliegt. Der Vergleich über mehrere Modelle hinweg ist nur in besonderen Situation möglich (wenn die Modelle nested sind).

Man kann natürlich auch X und Y Variablen transformieren.

ess_ger %>% 
  mutate(
    edu_z = scale(edu), 
    income_z = scale(income)
  ) %>%
  lm(income ~ edu_z, data = .)

## 
## Call:
## lm(formula = income ~ edu_z, data = .)
## 
## Coefficients:
## (Intercept)        edu_z  
##      5.8432       0.8829

Damit ist das Modell voll z-standardisiert. Die Interpretation wenn X um eine Standardabweichung ansteigt steigt y xxx Standarabweichungen. Nun liegt ein standardisierter Paramter vor der als \(\beta^*\) bezeichnet wird. Dieser ist im bivariaten Fall identisch zum Pearschon Korrelationskoeffizienten \(r\).

Alternativ kann man auch den unstandardisierten Parameter \(\beta\) gewichten um die Standardabweichungen der Variablen. Im multivariaten Fall liegt somit ein partiell geschätzter, z-standardisierter Parameter vor

\[ \beta^*=\beta\frac{s_{x}}{x_y} \]

Der Wertebereich von \(\beta^*\) reicht wie auch der von r von [-1,+1], mit \(mean=0\) und \(SD=1\). Dies entspricht allen standardisierten Variablen. \(\beta^*\) Werte größer oder kleiner als 1 kommen vor, bei sehr großem b und \(S_X > 2 S_Y\), z.B bei Multikolineraität. Im bivariaten Fall gilt \(\beta^*=r\), ebenso wie \(\beta^{*2}=r^2\). Der standardisierte Regressionskoeffizient gibt Auskunft über das Ausmaß der Veränderung der Y Variable auf einer Standardskala (mean=0 und sd=1).

3.7 OLS Schätzung

Bei einer lineare Regression werden die spezifizierten Parameter mit der OLS (Ordinary Least Squares) Methode geschätzt. Die Optimierung dieser Loss oder Fehlerfunktion berechnet im bivariaten Fall eine eine Regressionsgerade, welche die Summe der Abweichungsquadrate (Error) minimiert. OLS garantiert damit die BLUE Vorhersage (blaue Linie) mit dem durchschnittlich, kleinsten (quadratischen) Fehler (rote Linien).

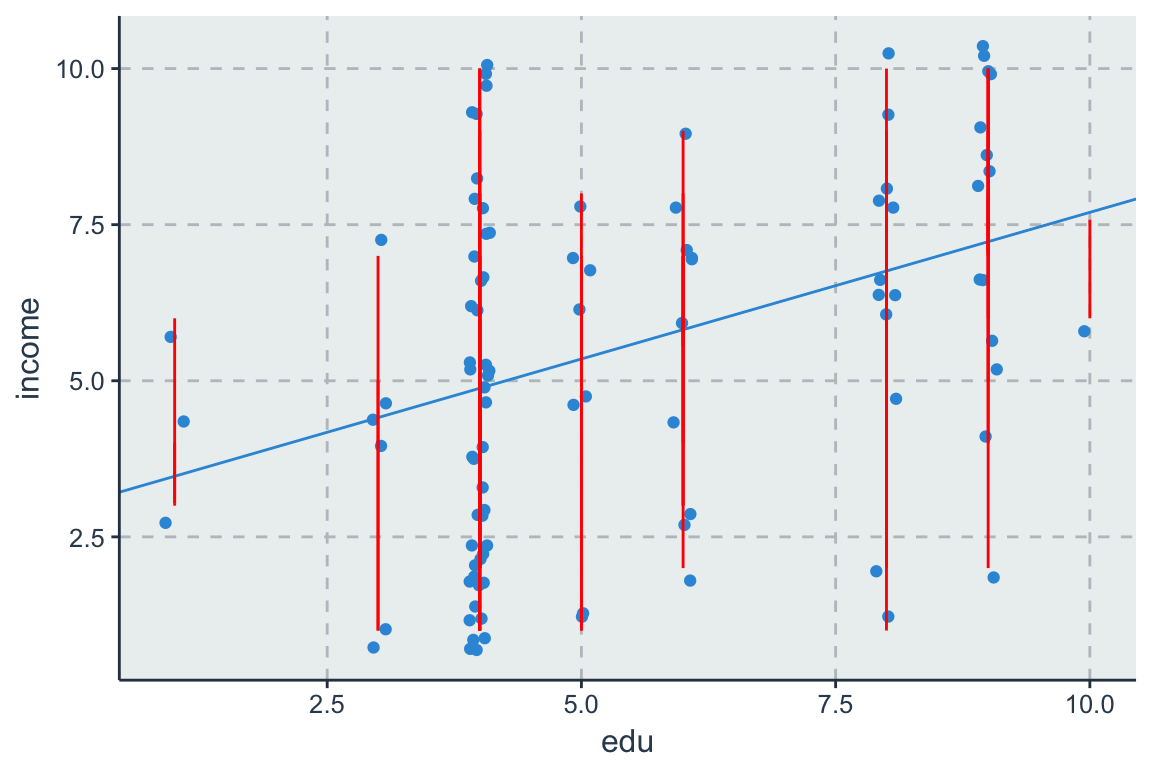
Die OLS-Schätzung kann wie folgt definiert werden

\[\ell(\beta) = \sum^N_{i = 1} (y_i - \hat y_i)^2\]

\[\ell(\beta) = \sum^n_{i = 1} (y_i - \beta_0 + \beta_1 x_i)^2 = \sum^n_{i = 1} \varepsilon_i^2 \]

Die Fehlerfunktion hat also dann ihren optimalen Punkt erreicht wenn die Summe der quadratischen Abweichungen minimal ist.

\[\hat \beta = argmin_\beta \;\;\ell(\beta)\]

Damit besitzt die OLS Schätzmethode folgende algebraische Eigenschaften, welche als BLUE Kriterien bekannt sind und in praktischer Form bei der Residuenanalyse zum Einsatz kommen.

1	\(\frac{1}{n}\sum^n_{i = 1}\varepsilon_i^2 = 0\)	Der Stichprobenmittelwert der Residuen ist Null
2	\(\frac{1}{n}\sum^n_{i = 1}x_i\varepsilon_i = 0\)	Die Stichprobenkovarianz zwischen dem Regressor und dem Residuum ist Null.
3	\(\bar y = \beta_0 + \beta_1 \bar x\)	Die Stichprobenmittelwerte \(\bar y\) und \(\bar x\) liegen auf der Regressionsgerade
4	\(\frac{1}{n}\sum^n_{i = 1}\hat y_i\varepsilon_i = 0\)	Die Stichprobenkovarianz zwischen \(\hat y_i\) und \(\varepsilon_i\) ist Null.

Weitere Schätzmethoden:

Maximum-Likelihood
Restricted ML
MAD
Gradient Boosting
Any other Liklihood function